Quantum capacitance

Quantum capacitance (density) is a physical value first introduced by Serge Luryi (1988)^[1] to describe the 2D-electronic systems in silicon surfaces and AsGa junctions. This capacitance was defined through standard density of states in the solids. Quantum capacitance could be used in the quantum Hall effect (integer and fractional) investigations as a new approach which uses quantum LC circuit.

1 Theory
2 Experiments
3 Heterostructure tunnel junctions
4 Graphene MOSFETs
5 References
6 External links

Theory

In the general case 2D-density of states in a solid could be defined by the following:

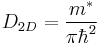$D_{2D} = \frac{m^*}{\pi \hbar^2} \$ , (1)

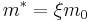where $m^* = \xi m_0$ is a current carrier's effective mass in a solid, 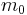$m_0$ is the electron mass, and $\xi$ is a dimensionless parameter which considers the zone structure of a solid. So, the quantum capacitance can be defined as follows:

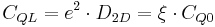$C_{QL} = e^2\cdot D_{2D} = \xi \cdot C_{Q0}$ , (2)

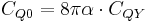where $C_{Q0} = 8\pi \alpha \cdot C_{QY} \$ - the ‘‘ideal value’’ of quantum capacitance at 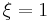$\xi = 1 \$ and another ideal quantum capacitance:

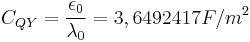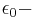$C_{QY} = \frac{\epsilon_0}{\lambda_0} = 3,6492417 F/m^2 \$ , (3)

where $\epsilon_0 - \$ dielectric constant, 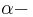$\alpha - \$ fine structure constant and 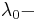$\lambda_0 - \$ Compton wave length of electron, first defined by Yakymakha (1994) )^[2] in the spectroscopic investigations of the silicon MOSFETs.

Experiments

Heterostructure tunnel junctions

The first attempt of quantum capacitance experimental confirmation in the 21st century were made by Qingmin Liu and Alan Seabaugh from the Notre Dame University (2001).^[3] They investigated GaAs heterostructure tunnel junctions. It is evident that tunnel junction capacity is defined by the metallurgic tunnel junction surface:

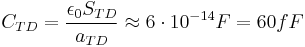$C_{TD} = \frac{\epsilon_0 S_{TD}}{a_{TD}} \approx 6\cdot 10^{-14}F = 60fF \$ (4)

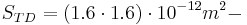where $S_{TD} = (1.6\cdot 1.6)\cdot 10^{-12} m^2 - \$ AlAs/InGaAs/AlAs- metallurgic tunnel junction surface, 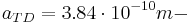$a_{TD} = 3.84\cdot 10^{-10}m - \$ junction thickness (its value could be estimated by heterostructure lattice constant). For the aim of comparison, the quantum capacitance (Yakymakha) in this case should be:

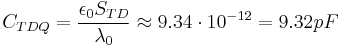$C_{TDQ} = \frac{\epsilon_0 S_{TD}}{\lambda_0} \approx 9.34 \cdot 10^{-12} = 9.32pF \$ .

Therefore this value is significantly greater than the experimental value obtained by Seabaugh. Thus, in the general case of tunnel junction, neither Yakymakha, nor Luryi (there are no 2D- density of states in the 1D- dimension) approaches could be used.

Graphene MOSFETs

One publication on the theme was made by Zhihong Chen and Joerg Appenzeller^[4] on the high quality Graphene field-effect transistor devices. In this paper the Luryi definition of quantum capacitance was used:

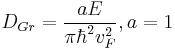$D_{Gr} = \frac{aE}{\pi \hbar^2v_F^2}, a = 1 \$ (5)

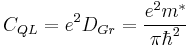$C_{QL} = e^2D_{Gr} = \frac{e^2m^*}{\pi\hbar^2}$ , (6)

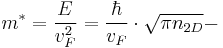where $m^* = \frac{E}{v_F^2} = \frac{\hbar}{v_F}\cdot \sqrt{\pi n_{2D}} - \$ current carriers cyclotron mass. The authors obtained the linear mirrors dependence of the quantum capacitance on the gate voltage, with the minimal value at the ‘‘Dirac point’’ about (Fig.7):

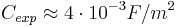$C_{exp} \approx 4\cdot 10^{-3} F/m^2 \$ .

In the case of the multi-layer graphene there is the constant value (independent of the gate voltage) of the quantum capacitance, equal to the minimal value of the mono-layer graphene. Further the authors supposed, that in the "ideal case" the quantum capacitance of graphene should have zero value at the Dirac point. This isn’t true. According to Yakymakha (1989),^[5] the 2D-system with the particles of two sorts have zone structure with the minimal particles concentration about the intrinsic value:

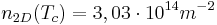$n_{2D}(T_c) = 3,03\cdot 10^{14} m^{-2} \$ . (7)

Using this value for the cyclotron mass, we obtain its minimum value:

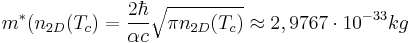$m^*(n_{2D}(T_c) =\frac{2\hbar}{\alpha c}\sqrt{\pi n_{2D}(T_c)} \approx 2,9767\cdot 10^{-33} kg \$ .(8)

Then, dimensionless parameter will be approximated as:

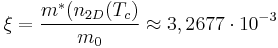$\xi = \frac{m^*(n_{2D}(T_c)}{m_0} \approx 3,2677 \cdot 10^{-3} \$ . (9)

From above, we can find out the minimal value of the quantum capacitance in graphene:

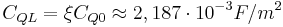$C_{QL} = \xi C_{Q0} \approx 2,187\cdot 10^{-3} F/m^2 \$ . (10)

This value is two times lesser than the experimental value. Nothing strange is there. Actually, we used above only one type of current carriers during estimation procedure. However, at the Dirac point in graphene, we have the two type conductivity, due to the quasi-electron and quasi-holes. Therefore, on practice, we have two quantum capacitances due to the quasielectron and quasiholes, connected in the parallel circuit. These two quantum capacitances confirms indirectly the existence of the “band structure” in graphene near the Dirac point with nonzero value of the “forbidden band”.

References

^ Serge Luryi (1988). "Quantum capacitance devices". Appl.Phys.Lett. 52(6). Pdf
^ Yakymakha O.L., Kalnibolotskij Y.M. (1994). "Very-low-frequency resonance of MOSFET amplifier parameters". Solid- State Electronics 37(10),1739-1751 pdf
^ Qingmin Liu and Alan Seabaugh (2001). "New Physical Understanding of the Resonant Tunneling Diode Small-Signal Equivalent Circuit". Notre Dame University Publications. Notre Dame University Publications Pdf
^ Zhihong Chen, Joerg Appenzeller (2008). "Mobility Extraction and Quantum Capacitance Impact in High Performance Graphene Field-effect Transistor Devices". Electron Devices Meeting, 2008. IEDM 2008. IEEE International. San Francisco, CA, USA. ISBN 978-1-4244-2377-4 [1]
^ Yakymakha O.L.(1989). High Temperature Quantum Galvanomagnetic Effects in the Two- Dimensional Inversion Layers of MOSFET's (In Russian). Kiev: Vyscha Shkola. p.91. ISBN 5-11-002309-3. djvu